Publication,
Research,
Docs and Info,
KAMEDA



Next: Experiment
Up: Multi-user live video
Previous: Video imaging for
Request of an user j is satisfied if a camera-work in 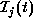 is selected and assigned to a certain camera at time t.
Suppose there are u users and c cameras. As a camera can
realize only one camera-work at a time, at most c camera-works can be realized
at time t. As a consequence, mediation for all the user requests is
necessary to select at most c camera-works among
is selected and assigned to a certain camera at time t.
Suppose there are u users and c cameras. As a camera can
realize only one camera-work at a time, at most c camera-works can be realized
at time t. As a consequence, mediation for all the user requests is
necessary to select at most c camera-works among 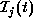 where
where
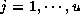 . Let us denote
. Let us denote 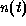 be the summed number of the
camera-works in
be the summed number of the
camera-works in 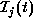 for all j.
If it includes the same camera-works,
they are counted as one camera-work.
The mediation is described
by the mediation matrix
for all j.
If it includes the same camera-works,
they are counted as one camera-work.
The mediation is described
by the mediation matrix 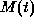 of
of 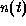 rows and u columns where
each component
rows and u columns where
each component 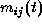 is either 1 or 0. A column represents
is either 1 or 0. A column represents
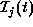 and a row corresponds one camera-work i.
and a row corresponds one camera-work i. 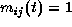 means that the user j realizes his/her request of the camera-work i.
Hence, the next inequality ought to be true for all j.
means that the user j realizes his/her request of the camera-work i.
Hence, the next inequality ought to be true for all j.
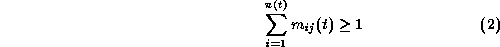
Note that at each column j, 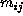 is always 0 if camera-work i is
not included by
is always 0 if camera-work i is
not included by 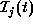 . We introduce
. We introduce 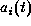 that indicates
whether the corresponding camera work of the ith row is selected or
not.
that indicates
whether the corresponding camera work of the ith row is selected or
not. 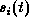 indicates the number of the users
who support the camera-work i.
indicates the number of the users
who support the camera-work i.
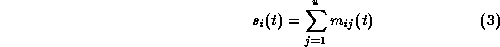
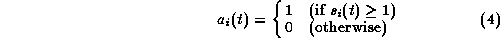
The constraint of the number of the cameras is formulated by
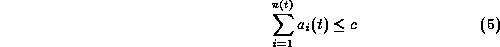
The mediation process is finding the mediation matrix M that
maximizes  under the constraints of Inequality
(2) and (5).
under the constraints of Inequality
(2) and (5).
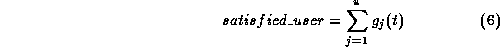
where 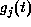 is defined as:
is defined as:
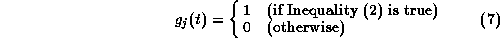
The mediation matrix 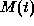 that satisfies
that satisfies 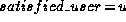 is
always found in the case
is
always found in the case 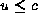 , but there might be a dynamic situation where
u > c and so
, but there might be a dynamic situation where
u > c and so 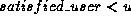 .
.
We use greedy algorithm to solve this problem. Although it does not
give us the best solution that maximizes 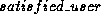 , it reaches
locally optimal solution with less amount of calculation, which is
essential in real-time processing.
, it reaches
locally optimal solution with less amount of calculation, which is
essential in real-time processing.
After the camera-works are selected, the next problem is to assign the
camera suitable to each selected camera-work under the constraint of the
camera location, direction and range. The criteria to solve this
problem is to satisfy the requests of the users as much as
possible. Our strategy is as follows.
- Order the selected camera-works by
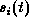 .
.
- Choose the best camera for each camera-work in the order.
In this way, the video image the user j watches is taken by
assigning the camera the selected camera-work in the mediation matrix
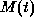 if his/her request is realized.
if his/her request is realized.
On the other hand, there might be a case where some users cannot
find their camera-works in the selected camera-works.
In this case, the user watches an arbitrary chosen video image.



Next: Experiment
Up: Multi-user live video
Previous: Video imaging for
Yoshinari Kameda
Fri Oct 1 16:26:35 JST 1999
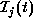 is selected and assigned to a certain camera at time t.
Suppose there are u users and c cameras. As a camera can
realize only one camera-work at a time, at most c camera-works can be realized
at time t. As a consequence, mediation for all the user requests is
necessary to select at most c camera-works among
is selected and assigned to a certain camera at time t.
Suppose there are u users and c cameras. As a camera can
realize only one camera-work at a time, at most c camera-works can be realized
at time t. As a consequence, mediation for all the user requests is
necessary to select at most c camera-works among 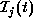 where
where
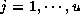 . Let us denote
. Let us denote 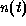 be the summed number of the
camera-works in
be the summed number of the
camera-works in 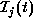 for all j.
If it includes the same camera-works,
they are counted as one camera-work.
The mediation is described
by the mediation matrix
for all j.
If it includes the same camera-works,
they are counted as one camera-work.
The mediation is described
by the mediation matrix 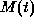 of
of 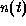 rows and u columns where
each component
rows and u columns where
each component 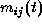 is either 1 or 0. A column represents
is either 1 or 0. A column represents
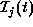 and a row corresponds one camera-work i.
and a row corresponds one camera-work i. 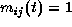 means that the user j realizes his/her request of the camera-work i.
Hence, the next inequality ought to be true for all j.
means that the user j realizes his/her request of the camera-work i.
Hence, the next inequality ought to be true for all j.
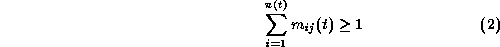
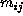 is always 0 if camera-work i is
not included by
is always 0 if camera-work i is
not included by 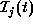 . We introduce
. We introduce 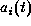 that indicates
whether the corresponding camera work of the ith row is selected or
not.
that indicates
whether the corresponding camera work of the ith row is selected or
not. 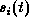 indicates the number of the users
who support the camera-work i.
indicates the number of the users
who support the camera-work i.
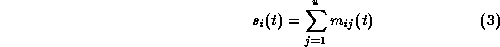
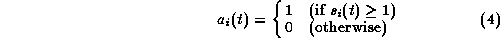
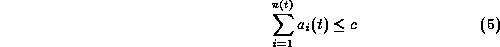
 under the constraints of Inequality
(
under the constraints of Inequality
(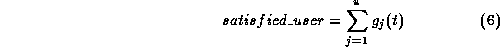
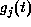 is defined as:
is defined as:
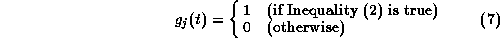
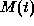 that satisfies
that satisfies 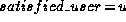 is
always found in the case
is
always found in the case 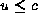 , but there might be a dynamic situation where
u > c and so
, but there might be a dynamic situation where
u > c and so 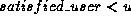 .
.
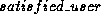 , it reaches
locally optimal solution with less amount of calculation, which is
essential in real-time processing.
, it reaches
locally optimal solution with less amount of calculation, which is
essential in real-time processing.
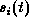 .
.
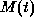 if his/her request is realized.
if his/her request is realized.